Les suites occupent une place essentielle dans l’enseignement de l’analyse.
Par exemple : un couple de lapins, né le premier janvier, donne naissance à un autre couple de lapins, chaque mois, dès qu’il a atteint l’âge de deux mois. Les nouveaux couples suivent la même loi de reproduction.
Combien y aura-t-il de couples de lapins le premier janvier de l’année suivante, en supposant qu’aucun couple n’ait disparu entre-temps ?
Pour résoudre ce problème de la reproduction des lapins, le mathématicien italien Fibonacci introduit dès 1202 la notion de suite.
Ainsi, si on note Un le nombre de couples de lapins au cours du mois (avec U1 = 1), la suite (Un) vérifie la relation de récurrence Un + 2 = Un + 1 + Un. On peut alors exprimer Un en fonction de n et prévoir le nombre de lapins au bout de quelques mois.
1. Suites arithmétiques
Une suite est arithmétique quand on passe d’un terme au suivant en ajoutant un même nombre (la raison que l’on note r).
D’où la formule de récurrence donnée pour tout entier n : (formule Un+1 en fonction de Un)
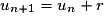
Le terme général d’une suite arithmétique est : (formule Un en fonction de n)
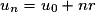 .
.
Cas particulier pour tout réel n, on a :
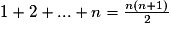 .
.
Pour démontrer qu’une suite (un) est arithmétique, il faut calculer la différence : 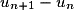
Si on obtient un nombre réel indépendant de n, alors la suite est arithmétique, sinon elle n’est pas arithmétique.
Remarque: pour calculer Un+1, il suffit de remplacer n par (n+1) dans la formule Un=f(n)
2. Suites géométriques
Une suite est géométrique quand on passe d’un terme au suivant en multipliant par le même facteur (la raison que l’on note q).
D’où la formule de récurrence donnée pour tout entier n : (formule Un+1 en fonction de Un)
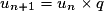
Le terme général d’une suite géométrique est : (formule Un en fonction de n)
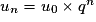
Enfin la somme des (n+1) premiers termes d’une suite géométrique (u0 + u1 +…+ un) de raison q différente de 1 est égale à :
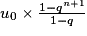
Pour tout réel q différent de 1, on a :
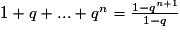 .
.
Pour démontrer qu’une suite (un) est géométrique, il faut calculer le rapport : 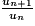
Si on obtient un nombre réel indépendant de n alors la suite est géométrique, sinon elle n’est pas géométrique.
Remarques:
– pour calculer Un+1, il suffit de remplacer n par (n+1) dans la formule Un=f(n)
– attention pour calculer un rapport, le dénominateur doit être différent de 0
3. Suite arithmético-géométrique
Définition : on dit qu’une suite (un) est une suite arithmético-géométrique s’il existe deux réels a et b tels que u0 étant donné, on a pour tout entier n : un+1 = aun + b.
On peut donc calculer chaque terme d’une suite arithmético-géométrique en utilisant les coefficients a et b et le terme précédent.
Exemple : en 2000 la population d’une ville était de 5 200 habitants. Chaque année la population augmente de 2 % mais 150 habitants quittent la ville. On note u0 le nombre d’habitants en 2000, et un le nombre d’habitants en 2000 + n.
Démontrer que la suite (un) est une suite arithmético-géométrique.
On sait qu’une augmentation de 2 % correspond à un coefficient multiplicateur de 1 + 2 % = 1,02.
On a u0= 5 200 et pour tout entier n : un+1 = 1,02un −150.
La suite (un) est donc une suite arithmético-géométrique.
Cas particuliers :
- si b = 0 et a est différent de 0, alors la suite est une suite géométrique de raison a ;
- si a = 1, alors la suite est une suite arithmétique de raison b.