Limites de fonctions

Déterminer des limites éventuelles d’une fonction n’a d’intérêt que lorsque x tend vers une borne ouverte de l’ensemble de définition Df de f.

Cette condition étant remplie, cela permet de connaître le comportement de f pour des valeurs de x proches de ces bornes ouvertes de Df.

C’est ainsi que l’on peut mettre en évidence la présence éventuelle d’asymptotes verticales ou horizontales à la courbe de f.

1. Opérations sur les limites

Soit f une fonction définie au voisinage de α. Ici α peut être un nombre réel, +∞ ou -∞

Limite d’une somme

Limite d’un produit

Limite d’une l’inverse

2. Comment lever une forme indéterminée ?

Les « ? » du paragraphe précédent signifient que l’on ne peut pas conclure directement : on est en présence d’une « forme indéterminée »

Pour « lever » cette indétermination, il faut transformer l’écriture de la fonction.
Voir méthode ici

3. Comment détermine-t-on la présence d’asymptotes à la courbe d’une fonction ?

Lorsqu’on est en présence d’une limite du type :

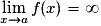
Asymptote verticale d’équation x=a

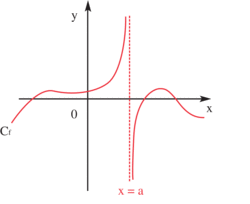
Lorsqu’on est en présence d’une limite du type :

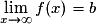
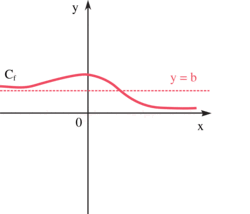
Asymptote horizontale d’équation y = b

 

4. Comment déterminer la limite d’une fonction en utilisant la comparaison ?

On peut utiliser les théorèmes de limite par comparaison.

Il y a trois cas. Soient f, g et h trois fonctions définies au voisinage de et soit l un nombre réel.

Premier cas : si g(x) ≤ f(x) et 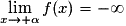alors:

alors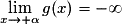 

Second cas : si g(x) ≥ f(x) et 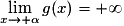alors:

alors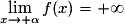 

Troisième cas : théorème des « gendarmes » : si f(x) ≤ k(x) ≤ g(x) et si:

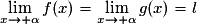  alors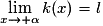 

Cas particuliers de la fonction exponentielle et de la fonction logarithme:

On peut utiliser les comparaisons directes :

pour tout réel x, on sait que x < exp(x) ;
pour tout réel x strictement positif : ln(x) < x.