Dérivation

Les calculs de dérivées ont de nombreuses applications : ils permettent de déterminer les variations d’une fonction, de résoudre des problèmes d’optimisation, de calculer certaines limites.

1. Qu’est ce qu’une fonction dérivable en un point ?

Une fonction f est dérivable en un réel a de son ensemble de définition si le taux d’accroissement de f en a admet une limite finie quand x tend vers a. Dans ce cas, ce réel est appelé « le nombre dérivé de f en a » et est noté f’(a).

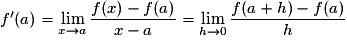On a : $f'(a)=\displaystyle \lim_{x\to a}\frac{f(x)-f(a)}{x-a}=\displaystyle \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$ .

S’il existe, f’(a) est le coefficient directeur de la tangente à la courbe représentative de la fonction f au point d’abscisse a.
Une fonction f est dérivable sur un intervalle I si elle est dérivable en tout réel a appartenant à I et on appelle « fonction dérivée de f » la fonction qui, à tout réel x appartenant à I, associe le réel f’(x).

2. Que faut-il retenir de la classe de Première ?

Tableau récapitulatif des formules à connaître

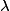u et v sont deux fonctions dérivables sur un intervalle de l’ensemble des réels, $\alpha$ et $\lambda$ deux réels quelconques:

3. Les nouvelles fonctions étudiées en classe de Terminale

La dérivée de la fonction x $\mapsto$ e^x est la fonction x $\mapsto$ e^x. Pour toute fonction u dérivable sur I,(e^u)’ = u‘e^u.

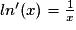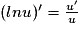Pour tout réel x > 0, on a $ln'(x)=\frac{1}{x}$ et pour toute fonction u dérivable strictement positive sur un intervalle I, $(lnu)'=\frac{u'}{u}$ .

Pour tout réel x : cos'(x) = − sin(x) et cos'(ax + b) = − a sin(ax + b).

Pour tout réel x : sin'(x) = cos(x) et sin'(ax + b) = a cos(ax + b).

4. Quelle est l’équation de la tangente à une courbe en un point où la fonction est dérivable ?

Si f est une fonction dérivable sur un intervalle I, alors le nombre dérivé de f en a appartenant à I, noté f’(a), est le coefficient directeur de la tangente T à la courbe C de f au point d’abscisse a.

Une équation de T est : y = f’(a)(x − a) + f(a).

5. Comment détermine-t-on le sens de variation d’une fonction dérivable sur un intervalle ?

Soit f une fonction dérivable sur un intervalle I. On note f’ sa dérivée sur I :

si f‘ = 0 sur I, alors f est constante sur I ;
si f‘ > 0 (respectivement f’ < 0) sur I, sauf éventuellement en un nombre fini de points isolés où f’ = 0, alors f est strictement croissante (respectivement décroissante) sur I.

À retenir

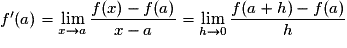$f'(a)=\displaystyle \lim_{x\to a}\frac{f(x)-f(a)}{x-a}=\displaystyle \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$ .
(e^u)’ = u‘e^u pour toute fonction u dérivable.
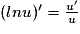$(lnu)'=\frac{u'}{u}$ pour toute fonction u dérivable strictement positive.
cos'(ax + b) = − a sin(ax + b) et sin'(ax + b) = a cos(ax + b).
Une équation de la tangente T est : y = f’(a)(x − a) + f(a).
Si f‘ > 0 (respectivement f’ < 0) sur I, sauf éventuellement en un nombre fini de points isolés où f’ = 0, alors f est strictement croissante (respectivement décroissante) sur I.

Le Coin des Maths