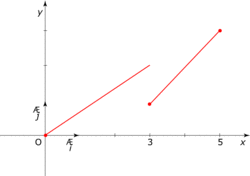
1. Comment reconnaît-on une fonction continue ?
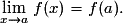
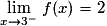 et
et 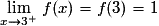 (les limites à gauche et à droite de la valeur 3 sont différentes).
(les limites à gauche et à droite de la valeur 3 sont différentes).
2. Qu’est-ce que la fonction partie entière ?
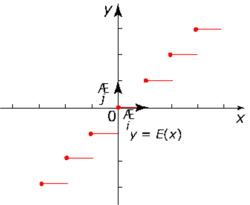
C’est l’occasion de découvrir une fonction qui n’est pas continue : la fonction partie entière notée E(x)
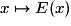 .
.Plus généralement, si x est encadré par deux entiers relatifs consécutifs n et n + 1, la fonction partie entière est définie par E(x) = n avec
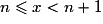 .
.Ainsi :
E(2,5) = 2 ; E(2) = 2 ; E(−2,5) = −3 car
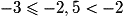 ; E(−3) = −3.
; E(−3) = −3.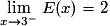 et
et 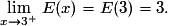
Les limites à gauche et à droite de 3 étant différentes, la fonction partie entière n’est pas continue en 3. Il en est de même pour toutes les valeurs entières.
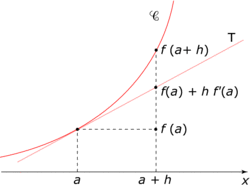
3. Une fonction continue est-elle toujours dérivable ? Une fonction dérivable est-elle toujours continue ?
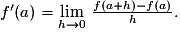
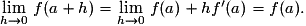
4. Continuité de fonctions de référence
Fonctions de référence :
* Les fonctions affines, polynômes, trigonométriques et valeur absolue sont continues sur R.
* Les fonctions rationnelles ( quotient de deux polynômes ) sont continues sur chacun des intervalles où elles sont définies.
* La fonction racine est continue sur ] 0 ; +∞ [
Et grâce aux propriétés qui suivent on peut s’appuyer sur la continuité de ces fonctions pour en déduire la continuité d’autres, en effet :
Toute somme, différence ou produit de fonctions continues sur I est continue sur I.
Le quotient u/v est continue sur I, si u et v sont continues sur I et si v ne s’annule pas sur I.
Remarque:
Si f est continue sur un intervalle I alors f est continue sur tout intervalle inclus dans I.
5. Théorème des valeurs intermédiaires
Maintenant que nous connaissons la notion de continuité, nous allons pouvoir étudier la dernière notion de ce chapitre, à savoir le théorème des valeurs intermédiaires (TVI)
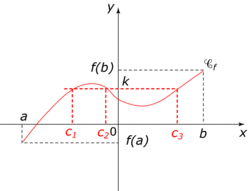
• Le théorème des valeurs intermédiaires s’énonce ainsi :
Soit f une fonction définie et continue sur un intervalle I, et a et b deux réels de I ;
Pour tout réel k compris entre f(a) et f(b), il existe (au moins) un réel c compris entre a et b tel que f(c) = k.
• Ce théorème a pour corollaire : si f est une fonction continue et strictement monotone sur un intervalle I alors, pour tout réel k de l’intervalle J = f(I), l’équation f(x) = k admet une unique solution dans I.
Note: Ce théorème sera très souvent utilisé lors de l’étude de fonctions, notamment avec l’équation f(x)=0 car il permettra ainsi d’étudier le signe de la fonction étudiée.