1.Suite (Un) est une fonction de n
Lorsque l’expression d’une suite s’apparente à celle d’une fonction définie sur R, où apparaît plusieurs fois l’entier naturel n, on peut considérer qu’il s’agit d’une somme, d’un produit ou d’un quotient de plusieurs suites. Soit par exemple (un) définie par un = n² + sin n ; on considérera qu’il s’agit de la somme d’une suite définie par vn = n² et d’une autre définie par wn = sin n.
Ainsi, certaines limites sont évidentes à déterminer. Elles sont résumées dans les tableaux ci-dessous (inutile de les apprendre par cœur, les résultats se trouvent facilement).
Il arrive aussi que des calculs complémentaires doivent être effectués pour arriver à trouver la limite d’une suite ! Ces situations sont indiquées sous l’abréviation FI (forme indéterminée).
Ci-dessous, m et m’ désignent deux réels.
Addition de 2 suites (Vn) et (Wn)

Produit de 2 suites (Vn) et (Wn)
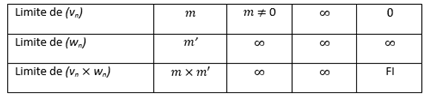
Bien sûr, la règle des signes permet de savoir si la limite est plus ou moins l’infini.
Quotient de 2 suites (Vn) et (Wn)
On considérera que (Vn) est un numérateur et (Wn) au dénominateur. On considérera aussi que m et m’ sont différents de 0.
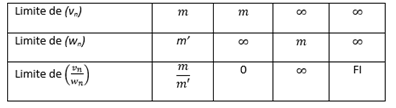
Lorsqu’à l’infini (Wn) tend vers 0, mais bien sûr sans jamais l’atteindre car le quotient n’aurait alors pas le bonheur d’exister, les limites sont les suivantes :
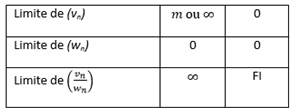
2. Lever une indétermination
Pour les formes indéterminées (FI) du type ∞-∞ et ∞/∞ , la méthode la plus courante consiste à factoriser par le plus haut degré de n.
Pour les additions et soustractions, il suffira de calculer un produit de limites après avoir fait la factorisation.
exemple:![]()
Pour les quotients par contre, il faudra simplifier l’expression factorisée avant de pouvoir calculer un quotient de limites.
exemple:
![]()
Après factorisation puis simplification cela donne:

Remarque:
Pour les suites dans lesquelles apparaissent une fonction racine carrée, la méthode courante de résolution d’une forme indéterminée consiste à multiplier l’expression par son expression conjuguée puis de calculer sa limite.
exemple:
![]()
Après transformation et multiplication par l’expression conjuguée cela donne:
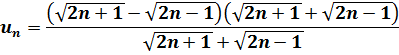
Après simplification:

